Question
Who among the following person attends the seminar just
after V? Study the following information carefully and answer the below questions. Ten persons namely –P, Q, R, S, T, U, V, W, X, and Y attend a seminar event in five different months viz.- January, April, July, September, December. Seminar in each month was scheduled on the 5thrd and 8th of the month. All the information is not necessary in the same order. The number of persons is attending a seminar after P is the same as the number of persons is attending the seminar before R. P attends seminar two months after Q, who attends the seminar on an odd date. R and Y attend the seminar in the same month. The number of persons is attending the seminar between Y and Q is the same as the number of persons is attending the seminar between P and X. The number of persons attending the seminar between U and R is one less than the number of persons is attending the seminar between W and V. U attends seminar three months before X, who attends seminar in one of the months has 31 days. V attends seminar on the 8th of the month but not in January. W and S attend seminars in the same month. At least two persons attend the seminar between T and P.Solution
The number of persons is attending a seminar after P is the same as the number of persons is attending the seminar before R. P attends seminar two months after Q, who attends the seminar on an odd date. R and Y attend the seminar in the same month. We will have four cases: If Q attends seminar on 5th January, then P will attend on 5th April. R will attend on 8 September and Y will attend on 5th September. If Q attends seminar on 5th April, then P will attend on 5th July. R will attend on 8 July but we do not have dates for Y. If Q attends seminar on 5th July, then P will attend on 5th September. R will attend on 8 April and Y will attend on 5th April. If Q attends seminar on 5th September, then P will attend on 5th December. R will attend on 8 January and Y will attend on 5th January.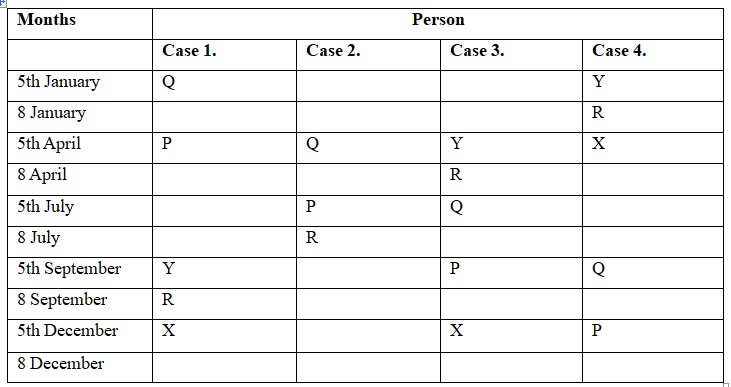 
The number of persons is attending the seminar between Y and Q is the same as the number of persons is attending the seminar between P and X. In case 1, there are five person between Q and Y. So, X attends seminar on 5th December. In case 3, there is one person between Q and Y. So, X attends seminar on 5th December. In case 4, there are five person between Q and Y. So, X attends seminar on 5th April. U attends seminar three months before X, who attends seminar in one of the months has 31 days. Case 1 and 4 will get discarded as we know that X attends the seminar in December and U should have attended in September. In case 3, U attends seminar on 8 September 
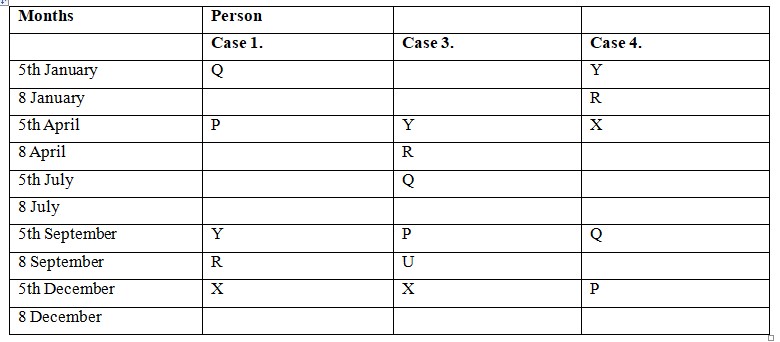At least two persons attend the seminar between T and P. So, T attends seminar on 8 December.   V attends seminar on the 8th of the month but not in January. Now it is clear that V attends the seminar on 8 July. The number of persons attending the seminar between U and R is one less than the number of persons is attending the seminar between W and V . W and S attend seminars in the same month. We know that three person are there between U and R. It means that there would have been four person between V and W. So, W and S attend seminar on 5th January and 8 January respectively. 
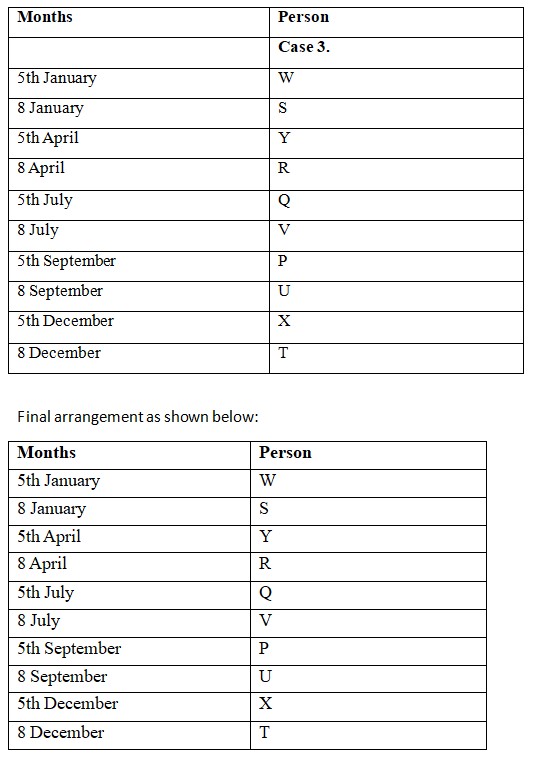Practice Next
Which heuristic search strategy uses both cost so far and estimated cost to goal?
The transfer function of the system below is ___________
You are designing a system where multiple threads need to access and modify a shared counter variable. What is a critical concern you must address to en...
What is Computer Output Microfilm (COM) primarily used for in data management and archival systems?
Which of the following is a common challenge in transitioning from a monolithic to a microservices architecture?Â
Predict the output
list1 = ['physics', 'chemistry', 1997, 2000]
list2 = [1, 2, 3, 4, 5, 6, 7 ]
print "list1[0]: ", list1[0]Â Â Â ...
To exit from a loop in shell we can use?
In object-oriented programming, when defining an interface method, which of the following statements is true regarding method parameters?
Attributes of a file can be :
When performing matrix multiplication (C = A \times B) in a code flow, if matrix A is m \times n and matrix B is n \times p, what is the time complexity...
Relevant for Exams:
