Question
As many persons completed between D and B is same as
between H and ___. Study the following information carefully and answer the questions given below. Eight persons A, B, C, D, E, F, G and H completed Army training in eight different years viz. 2012 to 2019, but not necessarily in the same order. D completed the training three years after F. Only three persons completed the training between C and F. C doesn’t complete on an odd numbered year. The number of persons completed before D is one more than the number of persons completed after B. Only one person completed the training between B and A. The difference between the years in which G and E completed is three years. Both H and E completed the training in consecutive years.Solution
We have, D completed the training three years after F. Only three persons completed the training between C and F. C doesn’t complete on an odd numbered year. From the above condition, there are three possibilities 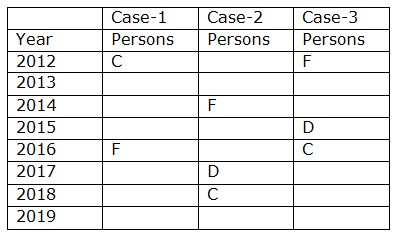 Again we have, The number of persons completed before D is one more than the number of persons completed after B. Only one person completed the training between B and A.
Again we have, The number of persons completed before D is one more than the number of persons completed after B. Only one person completed the training between B and A. 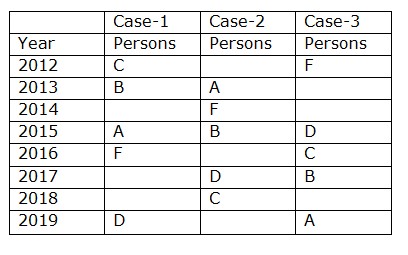 Again we have, The difference between the years in which G and E completed is three years. Both H and E completed the training in consecutive years. So Case2 and 3 get eliminated, hence the final arrangement becomes
Again we have, The difference between the years in which G and E completed is three years. Both H and E completed the training in consecutive years. So Case2 and 3 get eliminated, hence the final arrangement becomes 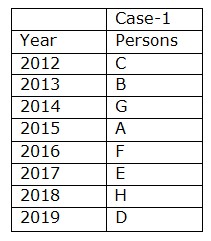
'A + B' means 'A is the wife of B'.
'A – B' means 'A is the father of B'.
'A × B' means 'A is the brother of B'.
'A ÷ B'...
How is E related to U?
Answer the questions based on the information given below.
There are eight persons J, K, L, M, N, O, P, and Q in a family of three generati...Four of the following five are alike in a certain way based on a group, which among the following does not belong to that group?
Who among the following is the son of the son in law of grandmother of F?
Sonam introduced a woman in a function, “She is the wife of the only son of my father’s brother’. How is the woman related to Sonam?
How is V related to R?
How is D related to E?
If N has only one child and there are four male members in the family then how is the child of N related to L?
Answer the questions based on the information given below.
Six persons M, N, O, P, Q and R live in a family of three generations. M is married ...
Relevant for Exams:


