Question
Which of the following Statements is true with respect
to the given information? Study the following information carefully and answer the questions given below: Six People – S, T, U, V, W, and X live in eight different floors of building (but not necessarily in the same order). Two of the floors in the building are vacant. The lowermost floor of the building is numbered one, the one above that is numbered two, and so on till the topmost floor is numbered eight. Each one of them likes a different brands of laptop, namely Apple, Lenovo, Xiaomi, Asus, Dell and HP (but not necessarily in the same order). All have a different number of books 2, 3, 4, 5, 6 and 8 but not in same order. The difference of books of T and X is equal to the number of books hold by W. The number of floors above W is same as the number of floors between W and U. W lives an odd numbered floor above the floor numbered four. There are three people live between the two vacant floors. Only three floors between U and the one who likes Asus. The one who likes Dell lives immediately above X. The difference of books of U and S is equal to the number of books hold by V. Only three floors between X and S. The one who likes HP lives immediately above the one who likes Apple. T has more books than X. T lives immediately above the one who likes Xiaomi. U has more books than S. The number of floors between W and the one who likes LENOVO is only one. The one who likes LENOVO Laptop immediately below one of the vacant floors. The floor number of the vacant floors are even – number. Only two floors are there between the one who likes HP and Asus. T lived immediately below one of the vacant floors and not on the ground floor. T neither lived on floor number 5 nor floor number 3. S has more than 3 books. The one who likes Lenovo lives on one of the floors below the floor number 4. X does not have 4 books. S has neither 2 nor 6 books. The number of books hold by T, X and W together is “4” less than the number of books hold by V, S and U together.Solution
W lives on an odd numbered floor above floor numbered 4. (so, there are 2 possible cases- either W lives on floor numbered 5 or 7). The no of floors above W are equal to number of floors between W and U. Only 3 floors are between U and Asus. 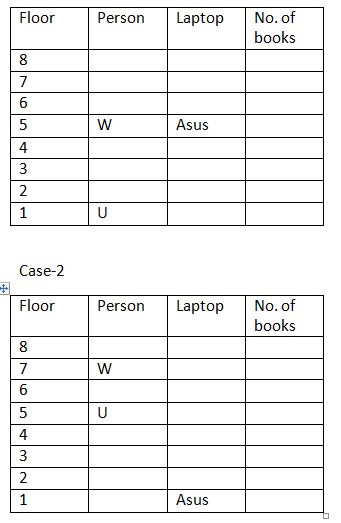 Only 2 floors are between Asus and HP. (so, we get another possible cases here). Case 1(a):
Only 2 floors are between Asus and HP. (so, we get another possible cases here). Case 1(a): 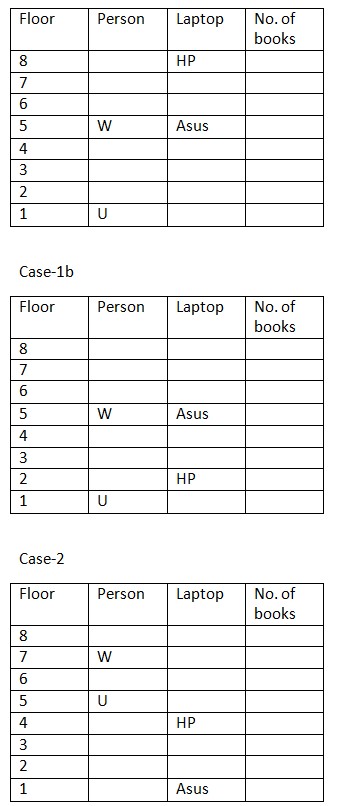 The one who likes HP lives immediate above Apple. There is one floor between W and lenovo. And it is also given that one who likes Lenovo lives somewhere below floor numbered 4. Floor immediately above one who likes Lenovo is vacant. (so, case 2 gets eliminated here). Case 1(a):
The one who likes HP lives immediate above Apple. There is one floor between W and lenovo. And it is also given that one who likes Lenovo lives somewhere below floor numbered 4. Floor immediately above one who likes Lenovo is vacant. (so, case 2 gets eliminated here). Case 1(a): 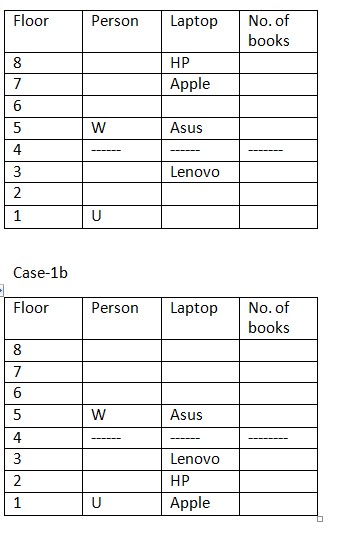 3 people live between 2 vacant floors and vacant floors are even numbered floors. (so, case 1(a) gets eliminated here as it does not satisfy the condition).
3 people live between 2 vacant floors and vacant floors are even numbered floors. (so, case 1(a) gets eliminated here as it does not satisfy the condition). 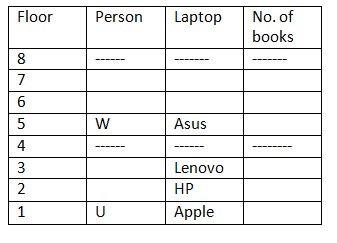 T lives immediately above the one who likes Xiaomi. X lives immediately below the one who likes Dell. Only 3 floors are between X and S.
T lives immediately above the one who likes Xiaomi. X lives immediately below the one who likes Dell. Only 3 floors are between X and S. 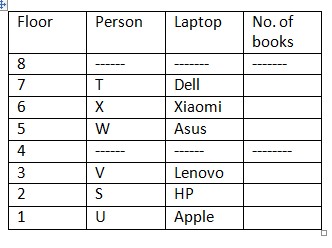 S has more than 3 books. And S has not 6 books. It is also given that U has more books than S. Difference between U and S books is equal to number of books V has.
S has more than 3 books. And S has not 6 books. It is also given that U has more books than S. Difference between U and S books is equal to number of books V has. 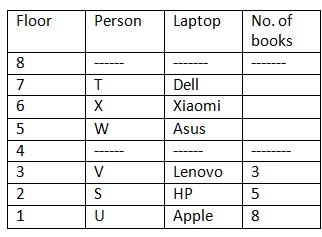 T has more books than X and difference between books of T and X is equal to books that W is having. X does not have 4 books.
T has more books than X and difference between books of T and X is equal to books that W is having. X does not have 4 books. 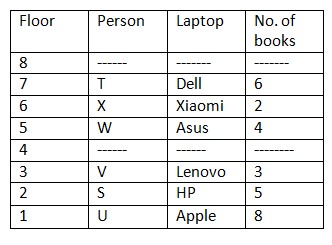
Who were the three new inductees into the ICC Hall of Fame in October 2024?
__________ defeated Japan to lift the trophy in the 2021 Hero Asian Champions trophy hockey in Dhaka.
The Asian Development Bank (ADB) cut India’s FY26 GDP growth forecast to what percentage?
Which public sector bank has launched the e-Bank Guarantee (e-BG) facility with National e-Governance Services Limited (NeSL) to reduce the time in loan...
Who inaugurated the Humayun's Tomb World Heritage Site Museum in New Delhi?
Why did the Indian government extend the tenure of the National Commission for Safai Karamcharis (NCSK) until 2028?
What is the length of a standard badminton court?
What are the broad contours of the Support for Poor Prisoners scheme?
Star Health Allied Insurance Company (Star Health) and Bajaj Allianz Life Insurance Company have partnered with which small finance bank to enable its c...
Which of the following statements about PM Modi's inauguration plans in Jammu is/are correct?
1. PM Modi will inaugurate the world's highest rail...
Relevant for Exams:


