Question
Four of the following five are alike in a certain way
as per the given arrangement and thus form a group. Find the one that does not belong to that group. Study the following information carefully and answer the question given below: Nine boxes viz. S, T, U, V, W, X, Y, Z and R are kept one above another but not in the same order. The box kept at the bottommost position is numbered as 1 and the box kept at the topmost position is numbered as 9. At most two boxes are kept below box U. Three boxes are kept between R and the box which is kept immediately above box U. W is kept two boxes above box R. Two boxes are kept between W and S. Box Z is kept immediately below box X. Box Y is kept three boxes below box X. Box T is kept above box V.Solution
We Have, At most two boxes are kept below box U. Three boxes are kept between R and the box which is kept immediately above box U. 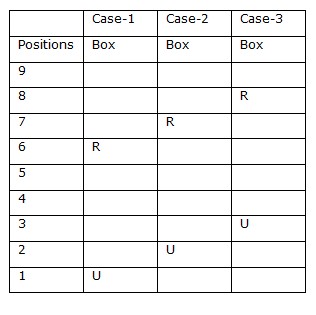 Again we have, W is kept two boxes above box R. Two boxes are kept between W and S.
Again we have, W is kept two boxes above box R. Two boxes are kept between W and S. 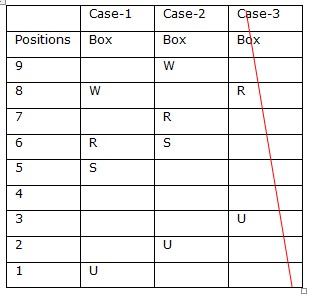 Case-III gets eliminated because no space left for W. Again we have, Box Z is kept immediately below box X. Box Y is kept three boxes below box X. Box T is kept above box V. Case-I gets eliminated because no space left for X and Y. So final arrangement is Case-2
Case-III gets eliminated because no space left for W. Again we have, Box Z is kept immediately below box X. Box Y is kept three boxes below box X. Box T is kept above box V. Case-I gets eliminated because no space left for X and Y. So final arrangement is Case-2 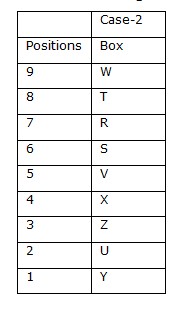
Select the figure from among the given options that can replace the question mark (?) in the following series.
Two statements are given, followed by four conclusions numbered I, II, III and IV.
Assuming the statements to be true, even if they seem to be...
Four letter-clusters have been given, out of which three are alike in some manner and one is different. Select the letter-cluster that is different.
There are three numbers, such that thrice the first number is equal to four times the second number and six times the third number. Find the ratio of th...
What should come in place of the question mark (?) in the given series based on the English alphabetical order?
GZK, JUJ, MPI, PKH, ?
...Four persons are painting a house. M is painting the front of the house. R is in the street behind the house painting the back. J is painting the window...
A man starts walking 10 meters east, then turns left and walks 5 meters. He then turns left again and walks 10 meters. He then again turns left and goes...
Select the option figure in which the given figure is embedded (rotation is NOT allowed).
Select the option figure in which the given figure (X) is embedded (rotation is NOT allowed).
What should come in place of the question mark (?) in the given series?
75 81 93 111 135 ?
Relevant for Exams:



