Start learning 50% faster. Sign in now
(i) Z lives on the fifth floor. (ii) V does not live on an odd – numbered floor and U lives below Z. Only W lives between V and U. (iii) There are three floors between the floors on which Y and W live. (iv) S lives on a prime numbered floor. There will be two cases: It is given that Z lives on the fifth floor. If V lives at floor no. 2, then W and U live at 3 and 4 respectively. Y lives at floor no. 7. If V lives at floor no. 4, then W and U live at 3 and 2 respectively. Y lives at floor no. 7. S lives at floor no. 11. 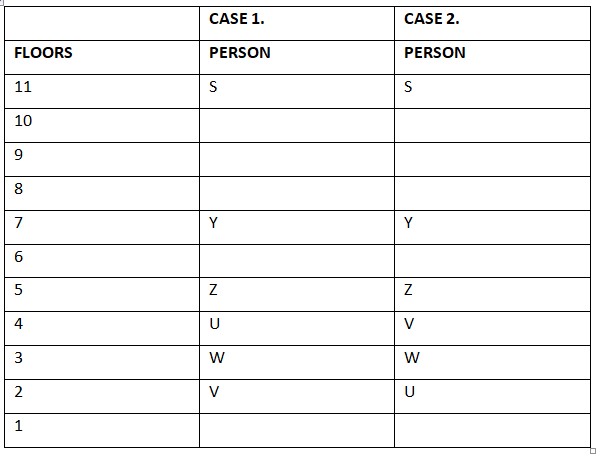 (v) None of the vacant floor is an odd-numbered floor. (vi) V does not live on a floor immediately above or immediately below X’s floor. There is one vacant floor between the floors on which S and T live. (vii) The number of floors between the two vacant floors is the same as the floor number on which W lives. (viii) X lives on an odd-numbered floor. X lives below T’s floor. R lives on an even numbered floor. T lives at floor no. 9 and vacant floor is floor no.10. We know that W lives at floor no. 3. So, there will be gap of three floors between vacant floors. Other vacant floor is floor no. 6. Case 1 will get discarded as X will live at floor no. 8 but X lives on an odd-numbered floor.
(v) None of the vacant floor is an odd-numbered floor. (vi) V does not live on a floor immediately above or immediately below X’s floor. There is one vacant floor between the floors on which S and T live. (vii) The number of floors between the two vacant floors is the same as the floor number on which W lives. (viii) X lives on an odd-numbered floor. X lives below T’s floor. R lives on an even numbered floor. T lives at floor no. 9 and vacant floor is floor no.10. We know that W lives at floor no. 3. So, there will be gap of three floors between vacant floors. Other vacant floor is floor no. 6. Case 1 will get discarded as X will live at floor no. 8 but X lives on an odd-numbered floor. 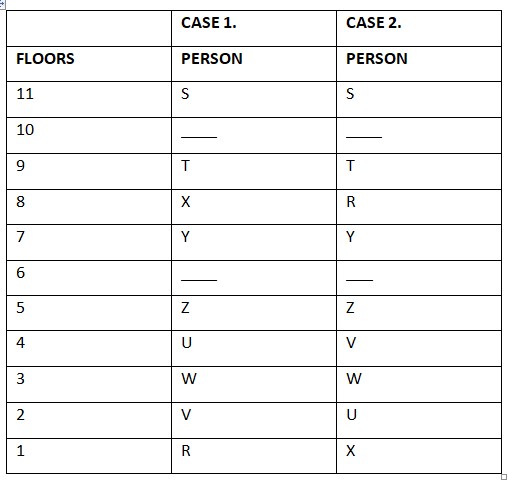 Final arrangement as shown below:
Final arrangement as shown below: 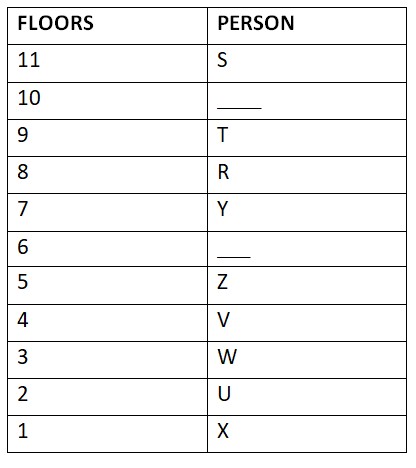
Find the approximate value of Question mark(?). There is no requirement to find the exact value.
(899.78 ÷ 15.11) × (√143.94 + 10.02) – 230...
(23.99)2– (17.99)2+ (1378.98 + 44.99) ÷ ? = 608
(9.013 – 15.04) = ? + 7.98% of 5199.98
111.89 × 4.12 – 504.04 ÷ 2.12 = 170.12 + ?
(284.85 ÷ 15.09) x 2.22 + 51.17 = 157.69 - ?
4650.12 ÷ √8648.88 + √27.08 * √1727.85 = ? – 609.10 ÷ 87.07
...15.1 + 3.97 – 9.07 × 1.96 = √?
90.004% of 9500 + 362 = ?
The average of 5 positive integers was initially computed as 30. However, it was discovered later that an error had occurred duri...
15.63% of 174.99 + √? = 139.98% of 24.98