Start learning 50% faster. Sign in now
From (i), if Vaani sits at place no. 1, then the girl having Samsung laptop sits at place no. 4. Iti is an immediate neighbour of Vaani, so she will sit either at place no. 8 or 2, but she cannot sit at place no. 2 because then person having Samsung will be to her right. Hence, Iti will sit at place no. 8 and the girls having Toshiba and Apple laptops will sit at place no. 6 and 2 respectively. 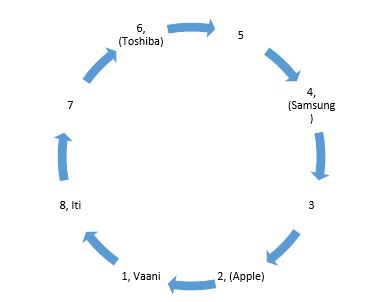 From (ii), Suman cannot sit at place no. 6, 5, 4 and 2. So, the places left for her are place nos. 3 or 7. From this, we get two possibilities: case (a) & case (b). In case (a), if Suman sits at place no.3, then Jaya will sit at place no. 6.
From (ii), Suman cannot sit at place no. 6, 5, 4 and 2. So, the places left for her are place nos. 3 or 7. From this, we get two possibilities: case (a) & case (b). In case (a), if Suman sits at place no.3, then Jaya will sit at place no. 6. 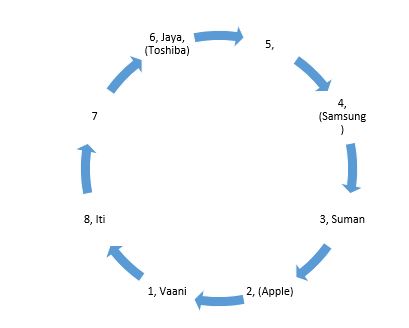 Case(a) In case (b), if Suman sits at place no.7, then Jaya will sit at place no. 2.
Case(a) In case (b), if Suman sits at place no.7, then Jaya will sit at place no. 2. 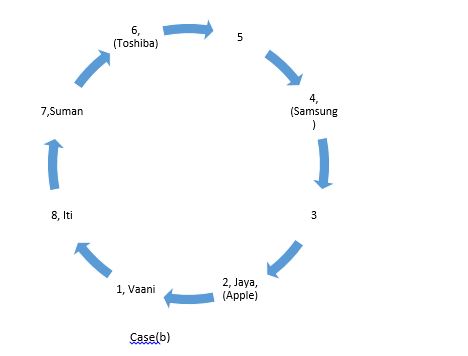 From (iii), it is clear for Kiran and Farah, two consecutive vacant places are required. . In case (a), two consecutive places are place no. 4 and 5, but since neither Kiran nor Farah is having Samsung laptop, so, case(a) is not possible. Hence, we will move forward with case(b). In case (b), two consecutive places for Kiran and Farah are place no. 6 and 5, but since the girl having Dell is second to the left of Kiran, Kiran cannot sit at place no. 6. Hence, it is clear that Kiran and Farah are at place nos. 5 and 6 respectively. It is also clear that the person having Lenovo is at 7 and the person having Dell is at 3.
From (iii), it is clear for Kiran and Farah, two consecutive vacant places are required. . In case (a), two consecutive places are place no. 4 and 5, but since neither Kiran nor Farah is having Samsung laptop, so, case(a) is not possible. Hence, we will move forward with case(b). In case (b), two consecutive places for Kiran and Farah are place no. 6 and 5, but since the girl having Dell is second to the left of Kiran, Kiran cannot sit at place no. 6. Hence, it is clear that Kiran and Farah are at place nos. 5 and 6 respectively. It is also clear that the person having Lenovo is at 7 and the person having Dell is at 3. 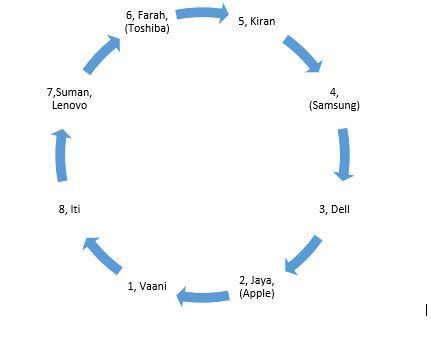 From (iv), it is clear that Heena will sit at place no. 3 and the girl having Compaq laptop will sit at place no. 8 i.e. Iti. So, Iti is having Compaq laptop and Heena is having Dell laptop. From(v), it is clear that the girl having Acer laptop is not an immediate neighbour of Samsung laptop, so Vaani is the one having Acer laptop and the only girl left for Samsung laptop is Geet. Only laptop is left is HP and only girl is left is Kiran. So, Kiran is having HP laptop.
From (iv), it is clear that Heena will sit at place no. 3 and the girl having Compaq laptop will sit at place no. 8 i.e. Iti. So, Iti is having Compaq laptop and Heena is having Dell laptop. From(v), it is clear that the girl having Acer laptop is not an immediate neighbour of Samsung laptop, so Vaani is the one having Acer laptop and the only girl left for Samsung laptop is Geet. Only laptop is left is HP and only girl is left is Kiran. So, Kiran is having HP laptop. 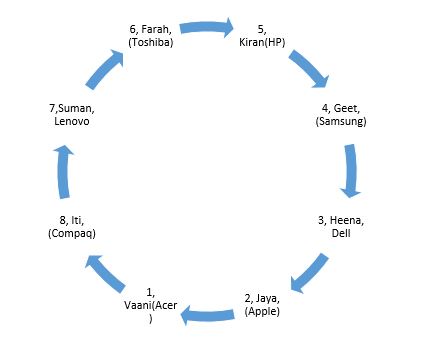
The Two Nations theory was propounded by Jinnah in :
Mahatma Gandhi returned to India from South Africa in _________.
The First Anglo-Burmese War was concluded with which treaty?
What does the Coolie Begar system in modern Indian history refer to?
Consider the following statements:
1. The teachings of Ramkrishna Paramhansa are characterized by the real-life issues of a common man.
With reference to the CWC meeting at Wardha (1939), consider the following statements:
1. Gandhi advocated unconditional support to the allied po...
Who was the founder of the Prarthana Samaj, a reformist movement in India?
Consider the following pairs with reference to the tribal uprising and their Leaders:
Which of the following rulers of the Gupta Empire is described as 'Maharajadhiraja'?
With reference to Raja Ram Mohan Roy, consider the following statements:
1. He established Atmiya Sabha as a part of Brahmo Samaj.
2. B...