Question
If L sits second to the left of I then how many seats
are between L and E when counted from the right of E? Study the following information carefully and answer the questions given below: A certain number of persons are sitting around the circular table. All of them are facing towards the center. Three persons sit between A and K who sits second to the left of C. E sits to the immediate left of G who sits second to the left of M. M sits third to the left of I who sits an immediate neighbour of K. Both E and A sit adjacent to each other. The number of persons sits between G and K is one less than the number of persons sits between K and E when counted from the right of both G and K respectively. At least one person sits between C and E when counted from the right of C.Solution
STEP I: M sits third to the left of I who sits an immediate neighbour of K. Three persons sit between A and K who sits second to the left of C. As per these statements, we can say that there are three possible cases and the arrangement will look like this: 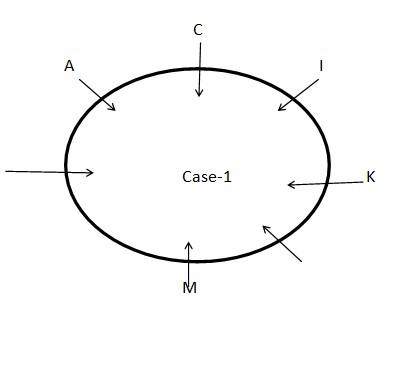
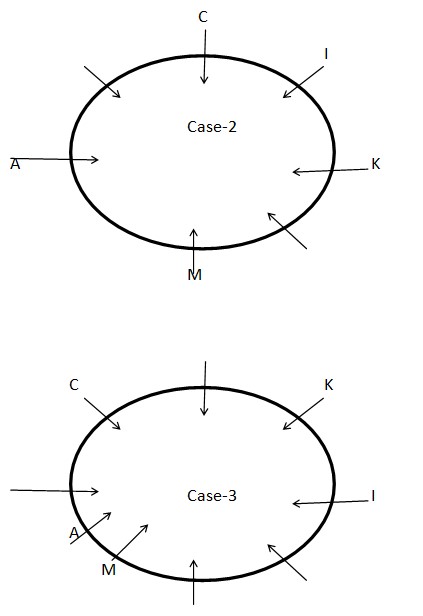 STEP II: E sits to the immediate left of G who sits second to the left of M. Both E and A sit adjacent to each other. The number of persons sits between G and K is one less than the number of persons sits between K and E when counted from the right of both G and K respectively. At least one person sits between C and E when counted from the right of C. As per these statements, CASE I and CASE III get eliminated and we continue with CASE II and the final arrangement will look like this:
STEP II: E sits to the immediate left of G who sits second to the left of M. Both E and A sit adjacent to each other. The number of persons sits between G and K is one less than the number of persons sits between K and E when counted from the right of both G and K respectively. At least one person sits between C and E when counted from the right of C. As per these statements, CASE I and CASE III get eliminated and we continue with CASE II and the final arrangement will look like this: 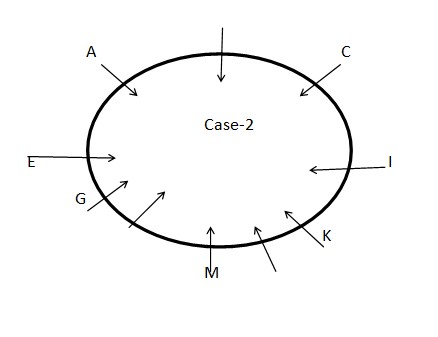
Which of the following parts of the stomach is called “True stomach”?
Green ear disease is associated to which of the following crops?
To raise incomes for farmers with enhanced production & productivity, Urea Gold was introduced. Urea Gold address which of the following challenges give...
ICAR- National Bureau of Animal Genetic Resources is situated at ___
The recently formed order with little profile development is termed as ………………………..
Which among the following method is the sexual method of Propagation?
Based on morphology, weeds are NOT classified as ________.
Which digital platform is promoted to provide farmers with a unified national market for agricultural commodities?
Which of the following crop is used for flax and oil both?
Which microbe is most commonly used in beverage industry to ferment malted cereals to produce ethanol (for the preparation of beer, rum etc.)?
Relevant for Exams:


