Question
Who sits 2nd to the left of
U? Answer the questions based on the information given below. Ten people O, P, Q, R, S, T, U, V, W and X are seated in two parallel rows such that five persons are seated in each row but not necessarily in the same order. Persons seated in row 1 are facing towards the east direction while persons seated in the row 2 are facing towards the west direction. Therefore, in the given seating arrangement persons seating in row 1 are facing and sitting opposite to the persons seating in row 2 and vice versa. X sits at one of the extreme ends and sits three places away from the one who faces S. P faces the one who sits to the immediate left of S. Only one person sits between P and T, who faces Q. U sits second to the left of Q and is sitting adjacent to the one who faces R. T is not sitting adjacent to R. Neither O nor V sits at the extreme ends. V neither faces west nor sits adjacent to U.Solution
X sits at one of the extreme ends and sits three places away from the one who faces S.P faces the one who sits to the immediate left of S. Only one person sits between P and T, who faces Q. Now, as X either sits extreme right or left end of row 1 or sits extreme right or left end of row 2 so, we have four possible places for X. 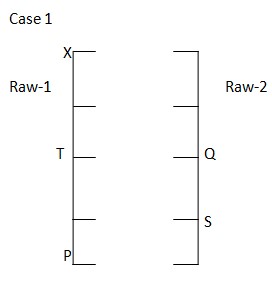
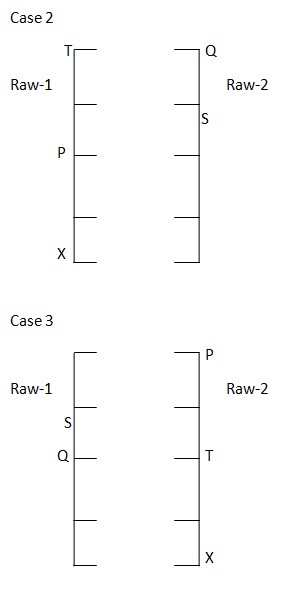
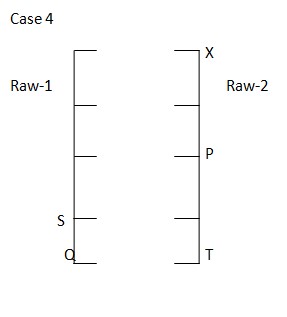 U sits second to the left of Q and is sitting adjacent to the one who faces R. T is not sitting adjacent to R. case I and III are invalid as R and T are not sitting together.
U sits second to the left of Q and is sitting adjacent to the one who faces R. T is not sitting adjacent to R. case I and III are invalid as R and T are not sitting together. 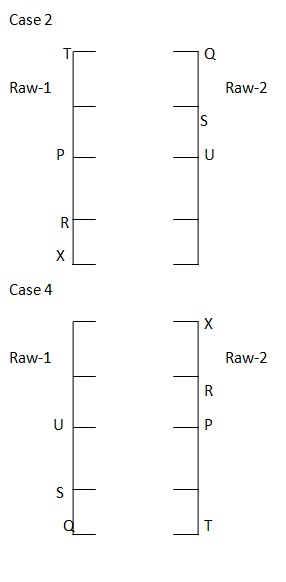 Neither O nor V sits at the extreme ends. V neither faces west nor sits adjacent to U. case IV is rejected as we can’t fix V in case IV. The final arrangement is as follows:
Neither O nor V sits at the extreme ends. V neither faces west nor sits adjacent to U. case IV is rejected as we can’t fix V in case IV. The final arrangement is as follows: 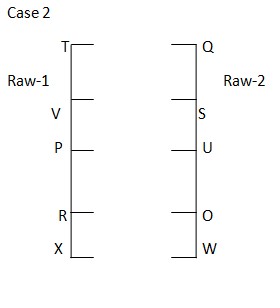
Select the phrase/connector/word-pair from the given three options to form a single sentence from the two sentences given below, implying the same meani...
- In each question, there are two statements which can be combined into a single statement in a number of different ways without changing their meaning. Belo...
Directions: Select the conclusion based on the meaning of the bold word.
Statement: You need to stop beating around the bush and answer dir...
In the following questions two statements have been given with connectors given below. You have to select an option that could connect both sentences...
(A) developing renewable energy sources
(B) is a key step towards reducing greenhouse gas emissions
(C) their lower environmental impact c...
In the question given below, a sentence is given with three blanks. Choose the correct combination of blanks that fit in the corresponding blanks. In t...
I was unwilling to go any further. I returned home.
(I) Returning home
(II) Though unwilling to return
(III) Unwilling to go
You're walking on thin ice by continuing to come in late. If the boss notices, you'll be fired.
Select the phrase/connector from the given three options which can be used to form a single sentence from the two sentences given below, implying the s...
In the following question, two statements and five connectors are given. Only one of the connectors from those given can be used to combine the given t...
Relevant for Exams:


