Question
Who is sitting second to the right of
P? Read the following information carefully and answer the questions given below it: Seven Persons J, K, L, M, N, O, P and Q are sitting around a square table in such a way that four of them who sits at the corner are facing towards the centre and other four who sits in the middle of the table are facing outside the centre. Each person has different number of coins viz. 11, 12, 13, 14, 15, 16, 17 and 18, but not necessarily in the same order. Only one person sits between Q and P. P sits second to the right of the person who has 18 coins. Q’s brother M, sits on the immediate left of his mother who has 16 coin. J is the father of P and only one person sits between Q’s mother and N. M’s daughter sits second to the right of O and on the immediate left of that person who has 13 coins. K sits second to the left of Q’s husband who has neither 14 nor 17 coins. O, who is sister of P, has 17 coins and is not an immediate neighbour of Q’s husband. N sits on the immediate right of the person who has 12 coins. M’s daughter has 11 coin. Only one person is sitting between J and O. No female is an immediate neighbour of K, who sits at the corner of the table. P is father of L and is not an immediate neighbour of N. J is married to Q.Solution
Q’s brother M, sits on the immediate left of his mother who has 16 coins. J is the father of P and only one person sits between Q’s mother and N. O, who is sister of P, has 17 coins and is not an immediate neighbour of Q’s husband. P is father of L and is not an immediate neighbour of N. J is married to Q. By the statement ‘only one person sits between Q’s mother and N’, we find that K is Q’s mother and N is M’ daughter. 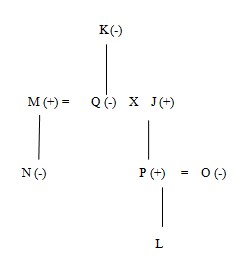 No female is an immediate neighbour of K, who sits at the corner of the table. K sits second to the left of Q’s husband who has neither 14 nor 17 coins. Only one person is sitting between J and O. M’s daughter sits second to the right of O and on the immediate left of that person who has 13 coins. N sits on the immediate right of the person who has 12 coins.
No female is an immediate neighbour of K, who sits at the corner of the table. K sits second to the left of Q’s husband who has neither 14 nor 17 coins. Only one person is sitting between J and O. M’s daughter sits second to the right of O and on the immediate left of that person who has 13 coins. N sits on the immediate right of the person who has 12 coins. 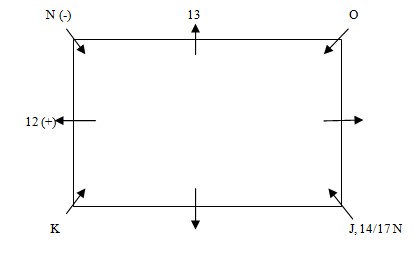 M, sits on the immediate left of his mother who has 16 coins. P is not an immediate neighbour of N. So, P can sit at immediate right or immediate left to J. If P sits immediate right to J, and as we know that Q is female so she sit at immediate left to N. We know that P sits second to the right of the person who has 18 coins. By this statement this condition is not possible. If P sits immediate left to J, so Q will sit at immediate right to J. Then L will sit at immediate left to N. Further P sits second to the right of the person who has 18 coins. It is given that N has 11 coin and that of O is 17. So P will have 14 and J will have 15 coins.
M, sits on the immediate left of his mother who has 16 coins. P is not an immediate neighbour of N. So, P can sit at immediate right or immediate left to J. If P sits immediate right to J, and as we know that Q is female so she sit at immediate left to N. We know that P sits second to the right of the person who has 18 coins. By this statement this condition is not possible. If P sits immediate left to J, so Q will sit at immediate right to J. Then L will sit at immediate left to N. Further P sits second to the right of the person who has 18 coins. It is given that N has 11 coin and that of O is 17. So P will have 14 and J will have 15 coins. 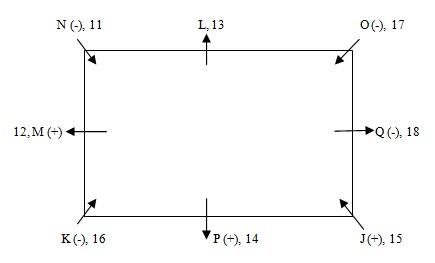
वर्तनी की दृष्टि से निम्नलिखित में से कौन सा शब्द अशुद...
नीचे दिया गया वाक्य चार भागों में बाँटा गया है ( A), (B), (C), और ( D) �...
वर्तनी की दृष्टि से निम्नलिखित में से कौन सा शब्द शुद्...
निम्नलिखित में से कौन सा वाक्य शुद्ध है?
आयकर जमा करने में / ही तुम्हारी भलाई है (b )/ और इससे तुम्ह�...
(1) अपने देश के कई भागों में इधर-उधर ताम्बा काफी मात्र�...
निम्लिखित में से शुद्ध शब्द छाँटिए
निम्न में कौन एक 'पर्वत' का पर्यायवाची शब्द है?
नीचे दिया गया वाक्य चार भागों में बाँटा गया है ( A), (B), (C), और ( D) �...
वाक्य के अशुद्ध भाग का चयन कीजिए –
Relevant for Exams:


