Question
Which of the following combination is not
true? Study the following information carefully and answer the questions given below it. Nine person namely – D, E, F, G, H, I, J, K and L lives in nine floored building marked 1 to 9 in such a way that lowermost floor is marked as 1, floor above it is marked as 2 and so on till topmost floor is marked as 9. Each person likes different fruit viz. Apple, Banana, Mango, Grapes, Papaya, Cherry, Strawberry, Orange and Kiwi. Each person also likes different vegetable viz. Patato, Tomato, Brinjal, Carrot, Peas, Cabbage, Radish, Capsicum and Pumpkin. All the given information is not necessary in same order. One who likes Radish lives on even numbered floor at a gap of three floors from one who likes Grapes. G, who doesn’t like Strawberry but likes Carrot, lives on floor just below the one who likes Grapes, who neither lives on floor marked as 6 nor on floor marked as 8. J, who doesn’t lives adjacent floor of K, lives on adjacent floor of one who likes Cherry. H, who doesn’t lives on floor adjacent to one who likes Orange, lives on odd numbered floor at a gap of one floor from one who likes Brinjal. Only one person lives between one who likes Apple and one who likes Radish. I who likes Capsicum lives on any floor below one who likes Strawberry. Only three person lives between one who likes Apple and K, who likes Pumpkin. F who likes Banana neither lives on adjacent floor of one who likes Radish nor one who likes Pumpkin. One who likes Carrot and Patato doesn’t lives on adjacent floor. Only two person lives between one who likes Banana and one who likes Kiwi. At least four person lives between one who likes Mango and Cherry, who lives on any floor above one who likes Radish. Only three person lives between one who likes Strawberry and one who likes Brinjal, who lives on adjacent floor of one who likes Patato. Only two person lives between D and one who likes Cabbage. One who likes Tomato lives on odd numbered floor just below one who likes Orange. E, who neither likes Papaya nor Radish, lives at a gap of one floor from one who likes Peas.Solution
One who likes Radish lives on even numbered floor at a gap of three floors from one who likes Grapes. G, who doesn’t like Strawberry but likes Carrot, lives on floor just below one who likes Grapes, who neither lives on floor marked as 6 nor on floor marked as 8, that means we have two different place for one who likes Grapes, in case (1) one who likes Grapes lives on floor marked 4, in case (2) one who likes Grapes lives on floor marked 2. Only one person lives between one who likes Apple and one who likes Radish, that means we have three different possible places for one who likes Apple, in case (1) one who likes Apple lives on floor marked 6, in case (2a) one who likes Apple lives on floor marked 8, in case (2b) one who likes Apple lives on floor marked 4. Only three person lives between one who likes Apple and K, who likes Pumpkin. Based on above given information we have 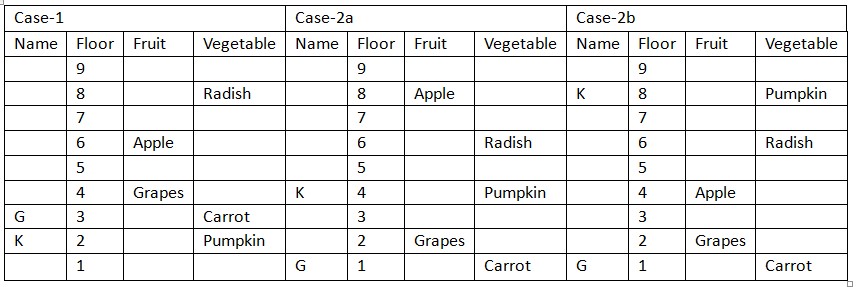 F who likes Banana neither lives on adjacent floor of one who likes Radish nor one who likes Pumpkin, that means in case (1) F lives on floor marked 5, in case (2a) F lives on top floor, in case (2b) F lives on floor marked 3. Only two person lives between one who likes Banana and one who likes Kiwi, that means we have four possible place for one who likes Kiwi, in case (1a) K likes Kiwi, in case (1b) one who likes Kiwi lives on floor marked 8, in case (2a) one who likes Kiwi lives on floor marked 6 and in case (2b) one who likes Kiwi lives on floor marked 8. One who likes Tomato lives on odd numbered floor just below one who likes Orange, that means in case (1a) one who likes Tomato lives on floor marked 7, in case (1b) one who likes Tomato lives on floor marked 1, in case (2a) one who likes Tomato lives on floor marked 3 and in case (2b) one who likes Tomato lives on floor marked 7.
F who likes Banana neither lives on adjacent floor of one who likes Radish nor one who likes Pumpkin, that means in case (1) F lives on floor marked 5, in case (2a) F lives on top floor, in case (2b) F lives on floor marked 3. Only two person lives between one who likes Banana and one who likes Kiwi, that means we have four possible place for one who likes Kiwi, in case (1a) K likes Kiwi, in case (1b) one who likes Kiwi lives on floor marked 8, in case (2a) one who likes Kiwi lives on floor marked 6 and in case (2b) one who likes Kiwi lives on floor marked 8. One who likes Tomato lives on odd numbered floor just below one who likes Orange, that means in case (1a) one who likes Tomato lives on floor marked 7, in case (1b) one who likes Tomato lives on floor marked 1, in case (2a) one who likes Tomato lives on floor marked 3 and in case (2b) one who likes Tomato lives on floor marked 7. 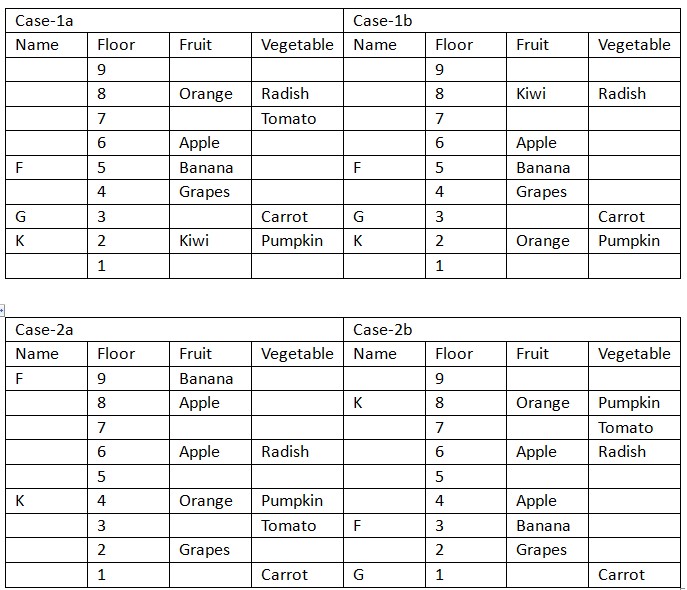 H, who doesn’t lives on floor adjacent to one who likes Orange, lives on odd numbered floor at a gap of one floor from one who likes Brinjal, that means case (1a) is not valid. Only three person lives between one who likes Strawberry and one who likes Brinjal, who lives on adjacent floor of one who likes Patato. One who likes Carrot and Patato doesn’t lives on adjacent floor, that means in case (1b) and (2a) H lives on floor marked 7, in case (2b) H lives on floor marked 5. I who likes Capsicum lives on any floor below one who likes Strawberry, that means in case (1b) I lives on floor marked 4, in case (2a) and case (2b) I lives on floor marked 2. Based on above given information we have:
H, who doesn’t lives on floor adjacent to one who likes Orange, lives on odd numbered floor at a gap of one floor from one who likes Brinjal, that means case (1a) is not valid. Only three person lives between one who likes Strawberry and one who likes Brinjal, who lives on adjacent floor of one who likes Patato. One who likes Carrot and Patato doesn’t lives on adjacent floor, that means in case (1b) and (2a) H lives on floor marked 7, in case (2b) H lives on floor marked 5. I who likes Capsicum lives on any floor below one who likes Strawberry, that means in case (1b) I lives on floor marked 4, in case (2a) and case (2b) I lives on floor marked 2. Based on above given information we have: 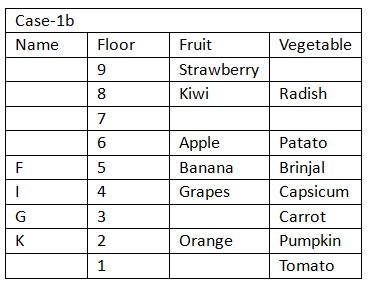
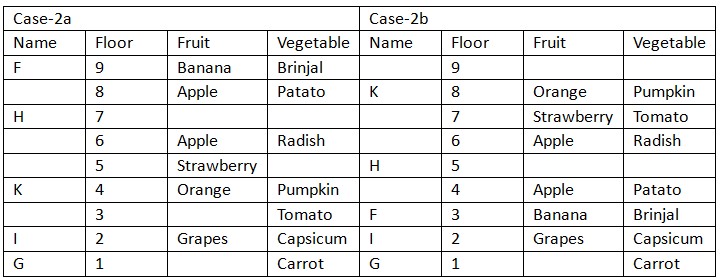 Case (1a) is not valid as H lives on odd numbered floor at a gap of one floor from one who likes Brinjal. Again, we have: J, who doesn’t lives adjacent floor of K, lives on adjacent floor of one who likes Cherry. At least four person lives between one who likes Mango and Cherry, who lives on any floor above one who likes Radish, that means case (1b) and (2b) is not valid and we have two possible places for J, in case (2a) J lives on floor marked 8 and in case (2c) J lives on floor marked 6. E, who neither likes Papaya nor Radish, lives at a gap of one floor from one who likes Peas, that means E lives on floor marked 5. Based on above given information we have:
Case (1a) is not valid as H lives on odd numbered floor at a gap of one floor from one who likes Brinjal. Again, we have: J, who doesn’t lives adjacent floor of K, lives on adjacent floor of one who likes Cherry. At least four person lives between one who likes Mango and Cherry, who lives on any floor above one who likes Radish, that means case (1b) and (2b) is not valid and we have two possible places for J, in case (2a) J lives on floor marked 8 and in case (2c) J lives on floor marked 6. E, who neither likes Papaya nor Radish, lives at a gap of one floor from one who likes Peas, that means E lives on floor marked 5. Based on above given information we have: 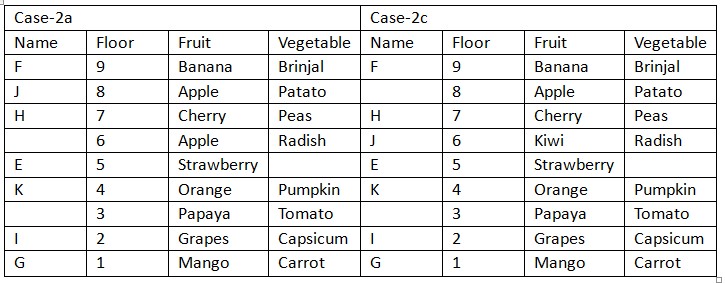 Case (1b) and case (2b) is not valid as one who likes Cherry lives on any floor above one who likes Radish. Again, we have: Only two person lives between D and one who likes Cabbage, that means case (2a) is not valid and in case (2c) D lives on floor marked 8. Based on above given information we have final arrangement as follow:
Case (1b) and case (2b) is not valid as one who likes Cherry lives on any floor above one who likes Radish. Again, we have: Only two person lives between D and one who likes Cabbage, that means case (2a) is not valid and in case (2c) D lives on floor marked 8. Based on above given information we have final arrangement as follow: 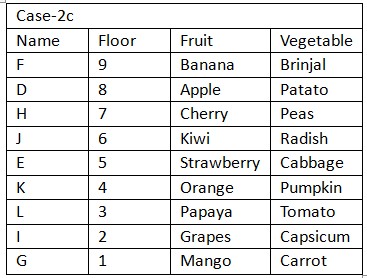
Which of the following statements is true about the one who likes Volvo?
If in a certain way ‘Red’ is related to ‘Banana’, Blue is related to ‘Grapes’ in the same way ‘Black’ is related to who among the follow...
How many box (es) were placed above the box which contained 35 Kg of Sugar?
Who among the following persons opted both Physics and Accountancy?
How many boxes are there between Y and X?
Which of the following is true regarding Aman?
Six friends D, E, F, G, H, and I go to a market on six different days of the same week from Monday to Saturday. E goes on Wednesday. D goes 3 days befor...
If C is related to 2015 and F is related to 2019 in a certain way, then G is related to which of the following year?
Which of the following statements is true about the one who likes Lava?
Four of the following five are alike in a certain way and hence form a group. Which among the following one does not belong to the group?
Relevant for Exams:



