Start learning 50% faster. Sign in now
Some whys are where (I) + All where are who’s (A) = Some whys are who’s.(I) ⇒ conversion ⇒ Some who’s are whys.(I) Hence, conclusion I will follow. A + I = No conclusion. Hence, neither conclusion II nor III follows. However, Conclusion II and III make a complementary pair, hence, either conclusion II or III follows. Alternative method: 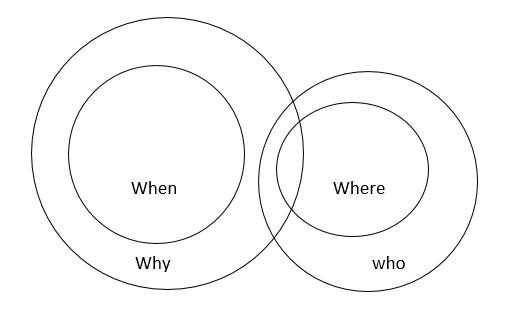
Which plant has stomata only on the upper surface of its leaves?
How many ATP molecules are required in the C₄ pathway for the synthesis of one molecule of glucose?
Which experiment demonstrated that food is translocated through the phloem?
Which type of sugar is most commonly transported during phloem translocation?
Agricultural census is conducted by Ministry of Agriculture and Farmers’ Welfare in every ___ year with participation of states and UTs since 1970 as ...
The first stable compound formed in the photosynthesis of C3 plants is:
The Structural and functional unit of chromosome is termed as
In the following given options, What is the importance of mitosis cell division?
Which statement about transpiration is true?
Which among the following is Photoblastic Seed?